SSC CGL 2021-13.04.2022-2 SSC Question Paper

SSC CGL 2021 Question Papers

SSC CGL 2021-13.04.2022-2 SSC Questions

51.
Quantitative Aptitude
A man bought toffees at 3 for a rupee. How many toffees for a rupee must he sell to gain 50%?
A.
4
B.
1
C.
3
D.
2
😑 View Answer Rough Work
ANSWER :
D. 2
52.
Chords AB and CD of a circle intersect externally at P. If AB = 7 cm. CD = 1 cm and PD = 5 cm, then the length of PB
A.
3
B.
10
C.
8
D.
5
😑 View Answer Rough Work
ANSWER :
A. 3
53.
In AABC, AB = 7 cm, BC = 10 cm, and AC = 8 cm. If AD is the angle bizector of BAC, where D is a point on BC. then DC (in cm) -?
A.
14/3
B.
16/3
C.
11/3
D.
17/3
😑 View Answer Rough Work
ANSWER :
B. 16/3
54.
A tyre has 3 punctures. The first puncture alone would have made the tyre flat in 9 minutes, the second alone would have done it in 18 minutes, the third alone would have done it in 6 minutes. If the air leaks out at a constant rate, then how long (in minutes) does it take for all the punctures together to make it flat?
A.
2
B.
6
C.
4
D.
3
😑 View Answer Rough Work
ANSWER :
D. 3
55.
The average of sixteen numbers is 48. The average of the first six of these numbers is 45 and that of the last seven numbers is 53. The seventh and the eighth numbers are, respectively, 3 and 7 greater than the ninth number. What is the average of the ninth and seventh numbers?
A.
41.5
B.
40.5
C.
42
D.
39
😑 View Answer Rough Work
ANSWER :
B. 40.5
56.
A sum of 4,620 is to be paid back in 2 equal annual instalments. How much is each instalment (in ₹) if the interest is compounded annually at 10% per annum?
A.
2420
B.
2552
C.
2662
D.
2750
😑 View Answer Rough Work
ANSWER :
C. 2662
57.

Study the pie chart and answer the questions that follow.
The pie chart represents the percentage-wise distribution of the total number of Vanilla cakes and Chocolate cakes sold every day in a week. The total number of cakes sold in a week = 10500.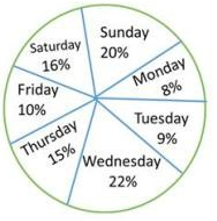
The ratio of the number of Vanilla cakes sold to the number of Chocolate cakes sold on Saturday is 4:3, the selling price of one Vanilla cake is ₹8 and that of one Chocolate cake is ₹15, then the total amount earned (in ₹) by selling all Vanilla cakes and Chocolate cakes on Saturday is:

A.

14880

B.

10488

C.

20000

D.

18480

😑 View Answer Rough Work
ANSWER :

D. 18480

58.

In the given figure, O is the centre of the circle. ∠POQ = 54º. What is the measure (in degree) of ∠PRQ?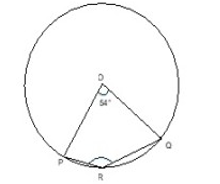

A.

235

B.

137

C.

207

D.

153

😑 View Answer Rough Work
ANSWER :

D. 153

59.
A train covers a distance of 225 km in 2 and a half hours at a uniform speed. The time taken by the train (in hours) to cover a distance of 630 km at the same speed is
A.
5
B.
7
C.
6
D.
4
😑 View Answer Rough Work
ANSWER :
B. 7
60.
A and B are two prime numbers such that A > B and their LCM is 209. The value of B² - A is:
A.
111
B.
102
C.
121
D.
109
😑 View Answer Rough Work
ANSWER :
B. 102