SSC CGL 2021-19.04.2022-2 SSC Question Paper

SSC CGL 2021 Question Papers

SSC CGL 2021-19.04.2022-2 SSC Questions

61.
A car covers a distance of 90 km in 50 min. What is its speed (in m/s)?
A.
60
B.
90
C.
108
D.
30
😑 View Answer Rough Work
ANSWER :
D. 30
62.
The compound interest on a certain sum of money at 21% p.a. for 2 years is ₹11,138.40 (interest compounded yearly). The total amount received (in ₹) after 2 years is:
A.
31538.4
B.
24000.5
C.
35138.4
D.
28315.4
😑 View Answer Rough Work
ANSWER :
C. 35138.4
63.
A 20 m long ladder rests against a wall so that the angle between the ladder and the wall is 30°. How far (in m) is the base of the ladder from the wall?
A.
10√3
B.
20√3
C.
20
D.
10
😑 View Answer Rough Work
ANSWER :
D. 10
64.
A and B had a joint business in which A invested ₹60,000 in the business for one year. After 3 months B invested Rs.80,000. At the beginning of the second year, A invested Rs.30,000 more and B withdrew Rs.5000. At the end of two years, profit earned by A is Rs.35,880. what is the profit (in ₹) earned by B, if they distributed half of the total profit equally and rest in the capital ratio?
A.
69920
B.
38060
C.
34040
D.
58940
😑 View Answer Rough Work
ANSWER :
C. 34040
65.

Study the given bar graph and answer the question that follows.
The bar graph shows the exports of cars of type A and B (in millions) from 2014 to 2018.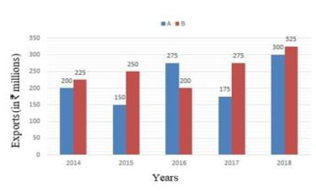
The total exports of cars of type B from 2015 to 2018 is what percentage more than the total exports of cars of type A from 2015 to 2018 (correct to one decimal place)?

A.

17.2%

B.

15.5%

C.

14.9%

D.

16.7%

😑 View Answer Rough Work
ANSWER :

D. 16.7%

66.
Two similar jugs have their heights of 8 cm and 12 cm, respectively. If the capacity of the smaller jug is 80 cm³, what is the capacity of the bigger jug (in cm³)?
A.
120
B.
192
C.
216
D.
270
😑 View Answer Rough Work
ANSWER :
D. 270
67.
The average of three numbers is 15. The average of the second and the third number is 12.5. What is the first number?
A.
18
B.
21
C.
24
D.
20
😑 View Answer Rough Work
ANSWER :
D. 20
68.
If cos B = 5/7, what is the value of cosec B + cot B? Given that 0 < B < π/2
A.
5/√6
B.
√6/12
C.
7/√6
D.
√6
😑 View Answer Rough Work
ANSWER :
D. √6
69.

The following pie-charts show the number of students studying in different departments of an institute during the academic years 2019 and 2020. The total number of students was 2000 and 2400, respectively, in academic years 2019 and 2020.
What is the ratio of the number of students studying science in the year 2019 to that in the year 2020?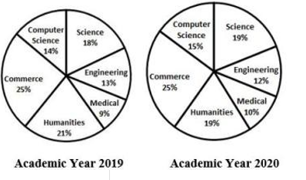

A.

18:19

B.

20:21

C.

15:19

D.

14:15

😑 View Answer Rough Work
ANSWER :

C. 15:19

70.

If cos 53° = x/y , then sec 53° + cot 37° is equal to:

A.

\(\tfrac{x + \sqrt{y^2 - x^2}}{y}\)

B.

\(\tfrac{x + \sqrt{y^2 - x^2}}{x}\)

C.

\(\tfrac{y + \sqrt{y^2 - x^2}}{x}\)

D.

\(\tfrac{y + \sqrt{y^2 - x^2}}{y}\)

😑 View Answer Rough Work
ANSWER :

C. \(\tfrac{y + \sqrt{y^2 - x^2}}{x}\)