If \(x-\dfrac{2}{x}=4\), then what will be the value of \(x^{2}+\dfrac{4}{x^{2}}\) ?
Study the given pie charts and answer the question that follows.
The pie charts represent the distribution of candidates who were enrolled for Bank Clerical Examination Fig (i) and the candidates (out of those enrolled) who passed the examination Fig (ii) in five different institutes P,Q. R, S and T.
(I) Total number of candidates enrolled in five different institutes = 5500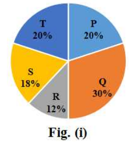
(II) Total number of candidates who passed the examination from five institutes = 3300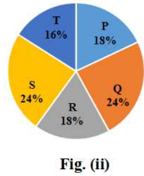
The ratio of the candidates who passed to the candidates enrolled from institute S is:
The number of students enrolled in different streams at Senior Secondary level in five schools has been shown in the bar graph. What is the ratio of the number of students enrolled in the vocational stream in schools A, C and E taken together to those enrolled in the humanities stream in the schools B, D and E taken together?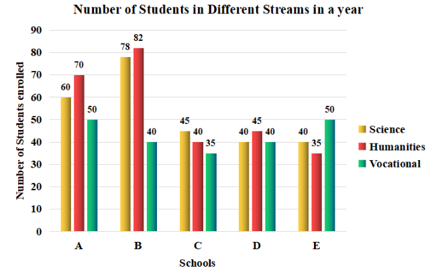
If \(x^{4}+\dfrac{1}{x^{4}}=3842\), then the positive value of \(x+\dfrac{1}{x}\) will be:
The value of \(31\dfrac{2}{5}\div\left[168\div\dfrac{3}{7}\text{ of }28+\left(33\div\dfrac{5}{2}\right)+\left(7\dfrac{3}{5}-3\dfrac{2}{5}\right)\right]\) is:
If cosec θ \(=\dfrac{41}{9}\) and θ is an acute angle, then the value of 5 tan θ will be:
\( \frac{11}{8} \)
\( \frac{13}{4} \)
\( \frac{7}{8} \)
\( \frac{9}{8} \)
The volume of a metallic cylindrical pipe is 3564 cm³. If its external radius is 12 cm and thickness is 3 cm, then the length of the pipe will be: \((\text{Take }\pi = \frac{22}{7})\)