SSC CHSL 2021-09.08.2021-2 SSC Question Paper

SSC CHSL 2021 Question Papers

SSC CHSL 2021-09.08.2021-2 SSC Questions

61.
Simplify the following expression.
A.
B.
C.
D.
41
😑 View Answer Rough Work
ANSWER :
D. 41
62.
If 5 cos θ = 4 sin θ, 0° < θ < 90°, then what will be the value of secθ ?
A.
B.
C.
D.
😑 View Answer Rough Work
ANSWER :
D. undefined
63.
If x + y = 27 and x2 + y2 = 425, then the value of (x - y)2 will be:
A.
225
B.
169
C.
121
D.
144
😑 View Answer Rough Work
ANSWER :
C. 121
64.
AB is the diameter of a circle of radius 9 cm. PQ is a chord (not a diameter) that intersects AB at M perpendicularly. If AM : BM = 5 : 4, then the length of chord PQ will be:
A.
5√5 cm
B.
6√5 cm
C.
6√3 cm
D.
8√5 cm
😑 View Answer Rough Work
ANSWER :
D. 8√5 cm
65.
The speed of a car is 40% more than that of a bus. A train covers 1020 km in 8 and a half hours. How much distance will the car cover in hours if the speed of the bus is half the speed of the train?
A.
164 km
B.
145 km
C.
147 km
D.
174 km
😑 View Answer Rough Work
ANSWER :
C. 147 km
66.
In a right-angled triangle ABC right angled at C, sin A = sin B. What is the value of cos A?
A.
B.
1
C.
D.
😑 View Answer Rough Work
ANSWER :
C. undefined
67.
Study the given graph and answer the question that follows.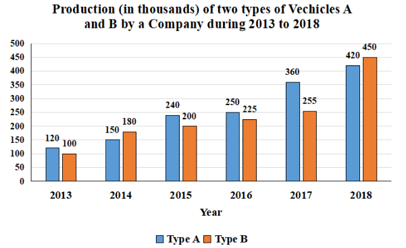
By what percentage (approximately) is the average number of vehicles of type B produced in 2014, 2016 and 2018 less than the number of vehicles of type A produced in 2017?
A.
21.4
B.
18.6
C.
20.8
D.
23.6
😑 View Answer Rough Work
ANSWER :
C. 20.8
68.
If two numbers are in the ratio 4 : 7 and the sum of their cubes is 407000, then the greater number will be:
A.
70
B.
63
C.
84
D.
77
😑 View Answer Rough Work
ANSWER :
A. 70
69.
The average pass percentage of girls in class X examination in a school is 85% and that of boys is 83%. The average pass percentage of all boys and girls in class X of that school is 83.7%. Find the percentage of the number of girls in class X of that school.
A.
35%
B.
30%
C.
45%
D.
40%
😑 View Answer Rough Work
ANSWER :
A. 35%
70.
AB is 12 cm long chord of a circle with centre O and radius 10 cm. The tangents at A and B intersect at P. What is the length of OP?
A.
12.5 cm
B.
12 cm
C.
10 cm
D.
2√61 cm
😑 View Answer Rough Work
ANSWER :
A. 12.5 cm