SSC CHSL 2021-12.04.2021-1 SSC Question Paper

SSC CHSL 2021 Question Papers

SSC CHSL 2021-12.04.2021-1 SSC Questions

51.
Section : Quantitative Aptitude
The line graph shows the production (in tonnes) and the sales (in tonnes) of a company. What percentage (approximately) of the total production of the company is the total sales of the company in all the years together? (correct to 2 decimal places)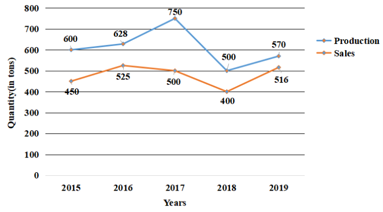
A.
75
B.
72.55
C.
68.12
D.
78.44
😑 View Answer Rough Work
ANSWER :
D. 78.44
52.
If cos θ = , then what will be the value of (sec θ + tan θ − cot θ sin θ)?
A.
B.
2 + √5
C.
D.
😑 View Answer Rough Work
ANSWER :
A. undefined
53.
One diagonal of a rhombus is 8√3 cm. If the other diagonal is equal to its side, then the area (in cm²) of the rhombus is
A.
12√3
B.
24√3
C.
16√3
D.
32√3
😑 View Answer Rough Work
ANSWER :
D. 32√3
54.
The average weight of 30 persons of group A is 3 kg more than the average weight of 25 persons of group B. The average weight of 25 persons of group B is 2.5 kg more than the average weight of 20 persons of group C. If the total weight of 30 persons of group A is 1725 kg, then what will be the average weight of the persons of group A and group C taken together (in kg)?
A.
55.3
B.
55.4
C.
55.1
D.
55
😑 View Answer Rough Work
ANSWER :
A. 55.3
55.
In △ABC, ∠A = 135°, CA = 5√2 cm and AB = 7 cm. E and F are the midpoints of sides AC and AB, respectively. The length of EF (in cm) is:
A.
6.5
B.
5.5
C.
6
D.
5
😑 View Answer Rough Work
ANSWER :
A. 6.5
56.
Study the given graph which shows the imports and exports of country XYZ during 2013 to 2018 (in crores Rs) and answer the question that follows.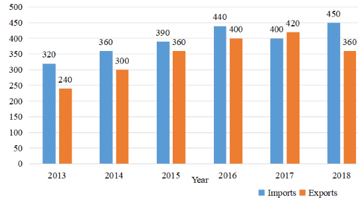
What is the ratio of the total exports in 2014 and 2017 to the total imports in 2015 and 2018?
A.
14:15
B.
3:2
C.
6:7
D.
5:6
😑 View Answer Rough Work
ANSWER :
C. 6:7
57.
If x² - 6√3x + 1 = 0, then the value of will be:
A.
234√3
B.
216√3
C.
666√3
D.
630√3
😑 View Answer Rough Work
ANSWER :
D. 630√3
58.
A car covers a distance of 48 km at a speed of 40 km/h and another 52 km with a speed of 65 km/h. What is the average speed of the car (in km/h) for the total distance covered?
A.
52.5
B.
50
C.
52
D.
53
😑 View Answer Rough Work
ANSWER :
B. 50
59.
Simplify the following expression:
(2x − 3y)³ - 18xy(2x − 3y)
A.
8x3 - 27y3 - 36x2y - 54xy2
B.
8x3 - 72x2y - 108xy2 - 27y3
C.
8x3 - 27y3
D.
8x3 + 108xy2 - 72x2y
😑 View Answer Rough Work
ANSWER :
B. 8x3 - 72x2y - 108xy2 - 27y3
60.
Anamika paid ₹4,965 as compound interest on a loan of ₹15,000 after 3 years when compounded annually. Suman took a loan of ₹10,000 at the same rate on simple interest. How much interest did Suman pay after 3 years?
A.
4500
B.
4000
C.
3000
D.
3500
😑 View Answer Rough Work
ANSWER :
C. 3000