SSC MTS 2021-05.10.2021-1 SSC Question Paper

The number of students taking admission in First Year of a Degree Course at a college in areas of Social Sciences in 2012 were as follows: Economics (S1) - 96, Psychology (S2) - 84, History (S3) - 160, Political Science (S4) - 120. Sociology (S9) - 125. The break-up of students in different subjects has been prevented through the given pie chart. Study the pie chart and answer the question that follows.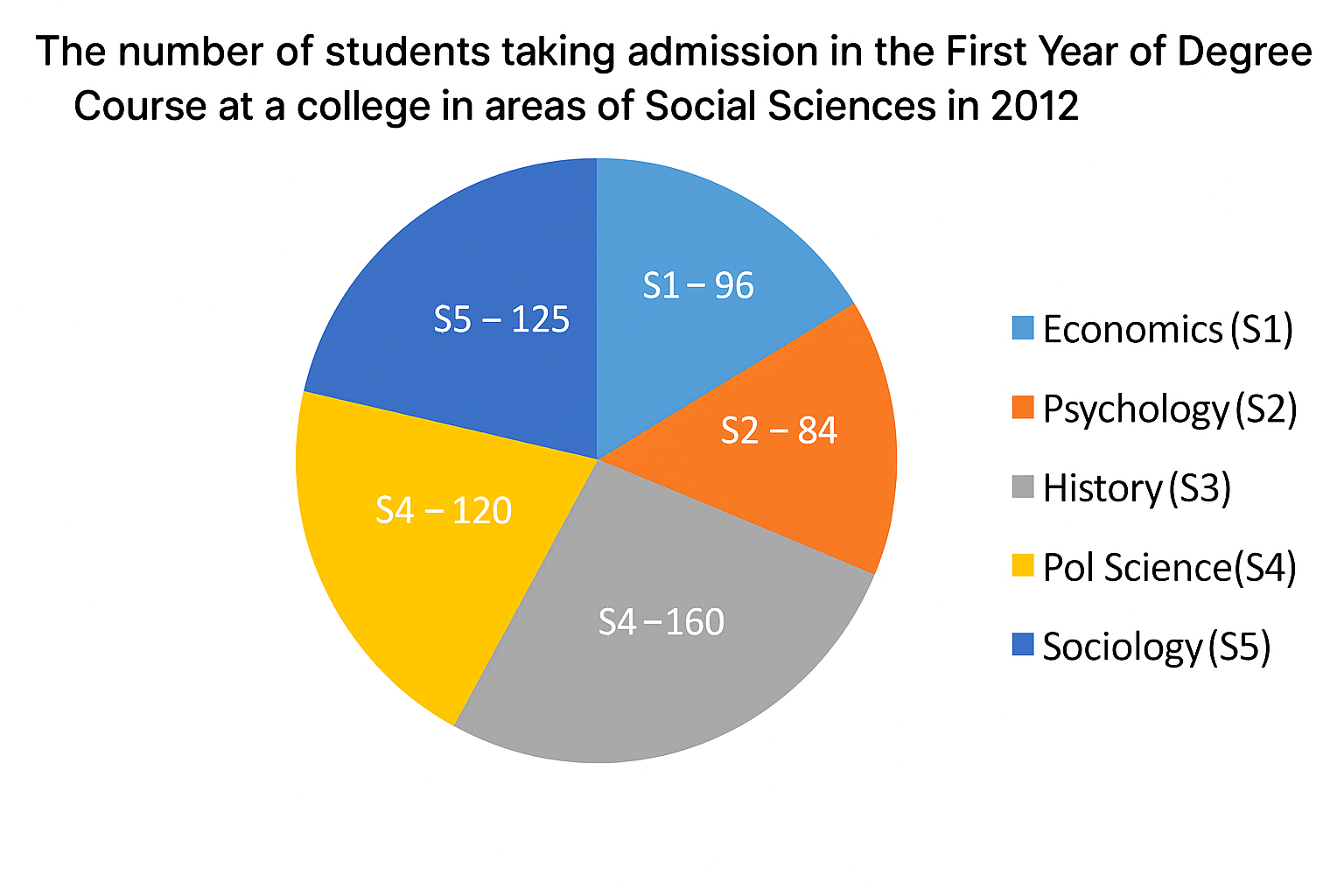
In 2013, 20% of the Sociology students, 25% of the Political Science students and one-sith of the Economics students shifted to another college, and the number of History students got increased by 10% doe to students shitting from other coleges. Over and above this, 10% of the remaining Sociology students and oor-seveuth of the Psychology students got transferred to Economics. What will be the central anzie (to the nearest dearce) of tho sector corresponding to History in the pie chart, representing the break-up in 2013?

The marked price of an article is Rs.400. A shopkeeper sells it by giving two successive discounts of 12% and 20% on its marked price. If he earns a profit of 10%, then the cost price of the article is?

Consider ten cousecutive odd numbers starting from 5. Multiply each of them, except the first and the secoad, with three. What will be the average of the ten numbers so formed?

A container in the shape of a right circular cone, wbose radius and depth are equal, gets completely filled by 128000 spherical droplets, each of diameter 2 mm. What is the radius (in cm) of the coatainer?

Study the given pie chart and naswer the question that follows.
The pie chart shows the distribution (degree-wise) of the number of players who play five sports A, B, C. D, aod E. (assuming each player plays only one sport)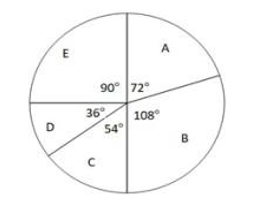
If the number of players who play sport C is 162, then the difference between the total number of players wbo play sports A and E is:

If I gain 124% by selling an item for Rs.1,232, then what would be my gain or loss percentage if I sell it for Rs.572?

Two men A and B, each working alone by working 12 hours per day, can complete a wok in 20 days. For executica of the work, it was decided that A and B would be working for 8 aod 6 hours per day, respectively, on alternate days startine with A. If it takes x days andy hours to complete the work then (x, y) is:

Simplify

How much time (in seconds) does the earth take to rotate through an angle of 135 degrees about its axis?

A fruit vendor brings 1092 apples and 3432 oranges to a market. He arranges them in heaps of equal number of oranges as well as apples such that every heap consists of the maximum possible number of the fruits. What is this number?