SSC MTS 2021-26.10.2021-3 SSC Question Paper

SSC MTS 2021 Question Papers

SSC MTS 2021-26.10.2021-3 SSC Questions

51.
Quantitative Aptitude
study the given pie chat, and answer the question that follows.
The given chart represents the percentage-wise distribution of the total number of vanilla cakes and chocolate cakes sold on each day of the week. The total number of cakes sold in a week = 10500.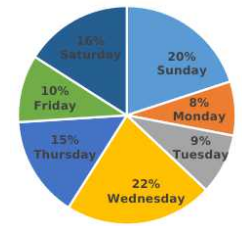
If the ratio of vanilla cakes sold to chocolate cakes sold on Wednesday is 13: 8, then how many vanilla cakes are sold on that day?
A.
1450
B.
1340
C.
1420
D.
1430
😑 View Answer Rough Work
ANSWER :
D. 1430
52.
If the ratio of the mean and median of a certain data is 4: 5, then the ratio of its mode and mean is:
A.
7:5
B.
6:5
C.
8:5
D.
7:4
😑 View Answer Rough Work
ANSWER :
D. 7:4
53.
An article was bought for ₹14,000 and sold at 4/7 of its cost price. The loss percentage is:
A.
42(3/7)%
B.
42(5/7)%
C.
42(6/7)%
D.
41(6/7)%
😑 View Answer Rough Work
ANSWER :
C. 42(6/7)%
54.
The average of four consecutive even numbers is 27. The smallest number is:
A.
20
B.
26
C.
24
D.
22
😑 View Answer Rough Work
ANSWER :
C. 24
55.
A can do a work in 7(1/2) days, whereas B can do the same work in 10(1/2) days. If they worked together, then the same work would be completed in
A.
4(3/8) days
B.
4 days
C.
4(1/2) days
D.
4(1/8) days
😑 View Answer Rough Work
ANSWER :
A. 4(3/8) days
56.
If a certain sum amounts ₹27,450 in 5 years at simple interest at the rate 10(1/2)% p.a., then the sum is:
A.
18000
B.
16500
C.
16000
D.
17000
😑 View Answer Rough Work
ANSWER :
A. 18000
57.
The value of
A.
-1
B.
0
C.
1
D.
-2
😑 View Answer Rough Work
ANSWER :
D. -2
58.
A loss of 12(1/2)% gets converted into a profit of 11(1/5)% when the selling price is increased by ₹118.5. The cost price of the article is:
A.
550
B.
600
C.
800
D.
500
😑 View Answer Rough Work
ANSWER :
D. 500
59.
Vineeth is younger than Vinoth by 8 years. If 4 years ago, their ages were in the ratio of 1 : 2, then the present age of Vinoth is:
A.
28 years
B.
22 years
C.
20 years
D.
25 years
😑 View Answer Rough Work
ANSWER :
C. 20 years
60.
The average speed of a train is 160% of the average speed of a car. The car covers a distance of 880 km in 16 hours. The time taken by the train to cover a distance of 484 km is:
A.
7(1/2) hours
B.
4(1/2) hours
C.
5(1/2) hours
D.
5 hours
😑 View Answer Rough Work
ANSWER :
C. 5(1/2) hours