SSC MTS 2022-22.07.2022-2 SSC Question Paper

SSC MTS 2022 Question Papers

SSC MTS 2022-22.07.2022-2 SSC Questions

61.
What is the value of
A.
26
B.
44
C.
50
D.
52
😑 View Answer Rough Work
ANSWER :
D. 52
62.
What is the value of
A.
-1891 / 691
B.
2075 / 693
C.
-1894 / 891
D.
-2075 / 693
😑 View Answer Rough Work
ANSWER :
D. -2075 / 693
63.

The following table shows the number of trains that originate in the five different zones of the railway network of a country.

Zone Trains
Z1 690
Z2 710
Z3 830
Z4 670
Z5 900

The total number of trains that originate in Z3 and Z4 taken together is what percentage of the total number of trains that originate in all the 5 zones taken together? 

A.

43.49%

B.

31.23%

C.

39.47%

D.

45.61%

😑 View Answer Rough Work
ANSWER :

C. 39.47%

64.
The following pie chart shows the expenditure of a village in a given year in the different sectors of its economy.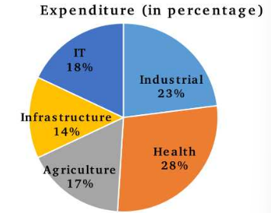
If the amount spent on agriculture was ₹8.5 crore, then find the amount spent in the IT sector.
A.
₹7.5 crore
B.
₹10.5 crore
C.
₹8 crore
D.
₹9 crore
😑 View Answer Rough Work
ANSWER :
D. ₹9 crore
65.
A sum of ₹3,400 is divided among P and Q in such a way that 3/4 of P's share is equal to 2/3 of Q's share. What is the positive difference between the shares of P and Q?
A.
500
B.
400
C.
200
D.
300
😑 View Answer Rough Work
ANSWER :
C. 200
66.
Profit earned on selling a book for ₹450 is the same as the loss incurred on selling it for ₹390. Find the cost price of the book.
A.
380
B.
460
C.
360
D.
420
😑 View Answer Rough Work
ANSWER :
D. 420
67.
The length, the breadth, and the height of a closed cardboard box are in the ratio of 5 : 3 : 7, respectively. Find the length of this box, if its total surface area is 1278 cm2
A.
20 cm
B.
15 cm
C.
25 cm
D.
10 cm
😑 View Answer Rough Work
ANSWER :
B. 15 cm
68.
If a sum of money amounts to 6 times of itself in 25 years at simple interest, then what is the rate of interest per annum?
A.
20%
B.
22.5%
C.
15%
D.
25%
😑 View Answer Rough Work
ANSWER :
A. 20%
69.
Train A crosses train B completely in 90 seconds, with the trains running in opposite directions. The lengths of the trains A and B are 900 metres and 1800 metres respectively. If the speed of train A is 45 km/h, then in how much time can train B cross a stationary pole?
A.
830/7
B.
810/7
C.
720/7
D.
650/7
😑 View Answer Rough Work
ANSWER :
C. 720/7
70.
Find the ratio of the simple interest and the compound interest on ₹100 at 10% per annum for 2 years, if, when compounded, interest is compounded annually
A.
13:32
B.
20:21
C.
21:20
D.
32:13
😑 View Answer Rough Work
ANSWER :
B. 20:21