In the following figure, if l ‖ m, then find the measures of angles marked by a and b.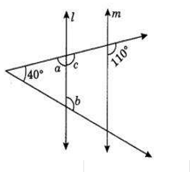
a = 90° and b = 90°
a = 55° and b = 125°
a = 70° and b = 110°
a = 60° and b = 120°
A and B can complete a piece of work in 13 and 17 days respectively. A begins to do the work, and they work alternatively one at a time for one day each. The whole work will be completed in:
\( 17\frac{11}{17} \) days
\( 17\frac{17}{19} \) days
\( 14\frac{11}{17} \) days
\( 11\frac{11}{17} \) days
There are two circles which touch each other externally. The radius of the first circle with centre O is 17 cm and the radius of the second circle with centre A is 7 cm. BC is a direct common tangent to these two circles, where B and C are points on the circles with centres O and A, respectively. The length of BC is:
\(2\sqrt{118}\,\text{cm}\)
\(2\sqrt{119}\,\text{cm}\)
\(2\sqrt{113}\,\text{cm}\)
\(2\sqrt{117}\,\text{cm}\)
The pie chart shows number of boys in 8 schools. The total number of boys is 10,000. Number of boys in a particular school is shown as a % of total number of boys in all these 8 schools.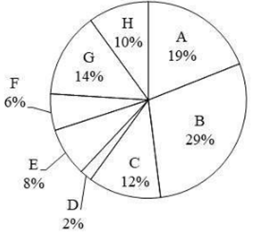
What is the ratio of total central angle formed by sector C, D and F to the total central angle formed by sector A, G and H?
If \(\, x + \frac{1}{x} = 2\sqrt{5} \,\) where x > 1, then the value of \(
\begin{aligned}
x^{3} - \frac{1}{x^{3}}
\end{aligned}
\)
if \(\tan A \tan B + \frac{\cos x}{\cos A \cos B} = 1, \text{ then } x = ?\)