SSC CGL 2022-13.12.2022-3 SSC Question Paper

SSC CGL 2022 Question Papers

SSC CGL 2022-13.12.2022-3 SSC Questions

61.
If, (r/13) + (13/r) = 1 then the value of r³ is:
A.
-2157
B.
2197
C.
2157
D.
-2197
😑 View Answer Rough Work
ANSWER :
D. -2197
62.
If (a/b) + (b/a) = -1 and a - b = 2, then the value of a3 - b3 is:
A.
0
B.
1/2
C.
1
D.
-1
😑 View Answer Rough Work
ANSWER :
A. 0
63.
A person borrowed 72,000 at 5% annual simple interest repayable in 3 equal annual installments. What will be the annual installment?
A.
Rs.730(10/63)
B.
Rs.840(9/61)
C.
Rs.640(11/63)
D.
Rs.250(10/63)
😑 View Answer Rough Work
ANSWER :
A. Rs.730(10/63)
64.
Two persons A and B working separately can sanitise a building in 6 and 10 hours, respectively. They work in stretches of one hour alternately. If A begins at 8 a.m., then when will the work be finished?
A.
9(1/3)h
B.
7(1/3)h
C.
6(1/3)h
D.
8(1/3)h
😑 View Answer Rough Work
ANSWER :
B. 7(1/3)h
65.
The area of two similar triangles are 324 cm² and 289 cm², respectively. What is the ratio of their corresponding altitudes?
A.
17/18
B.
17/19
C.
19/17
D.
18/17
😑 View Answer Rough Work
ANSWER :
D. 18/17
66.

The pie-chart shows marks of a student in different subjects out of 100.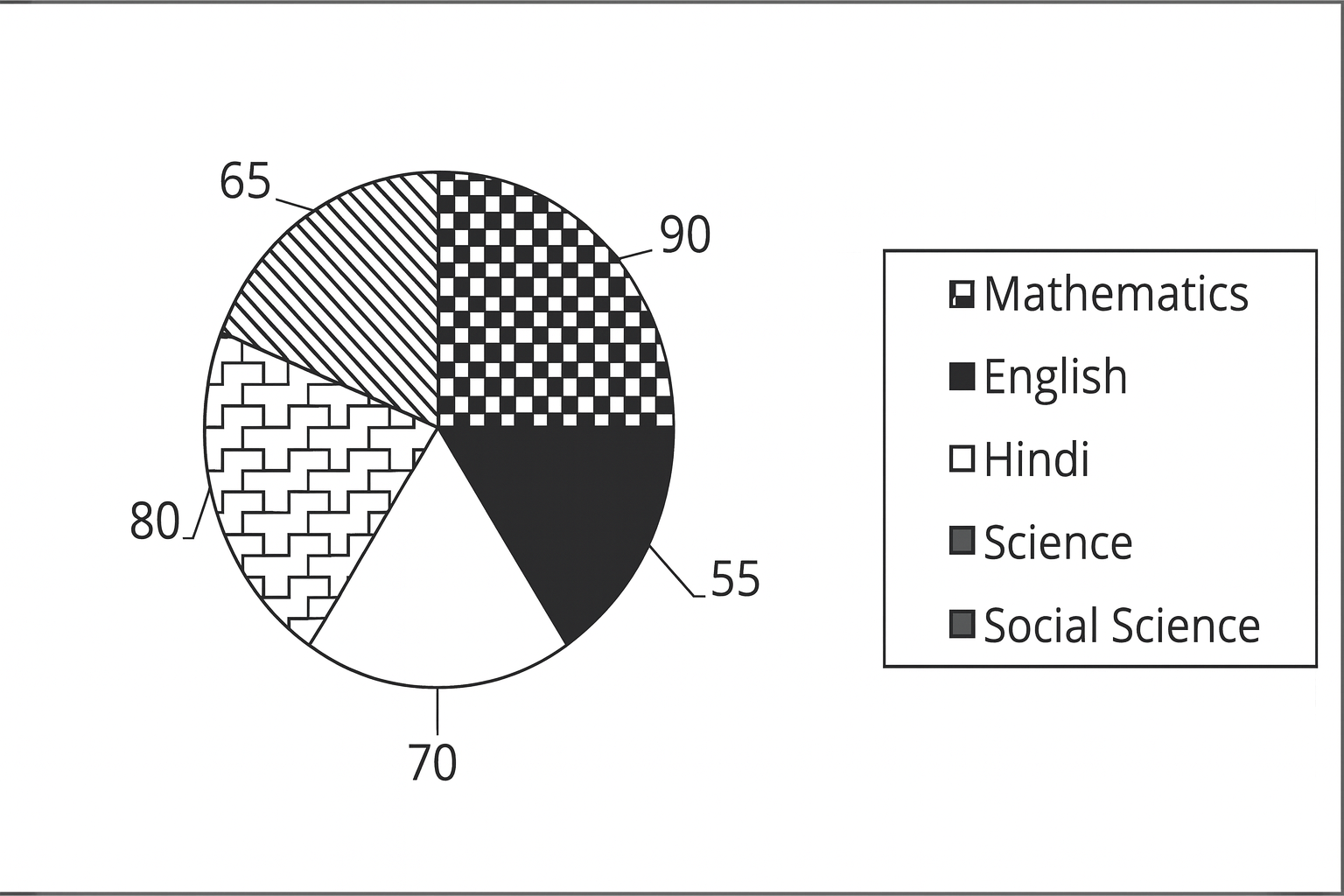
The marks scored in Hindi and Mathematics are more than the marks scored in English and Science by:

A.

35

B.

25

C.

20

D.

30

😑 View Answer Rough Work
ANSWER :

B. 25

67.
Train A running at 81 km/h takes 72 sec to overtake train B, when both the trains are running in the same direction, but it takes 36 sec to cross each other if the trains are running in the opposite direction. If the length of train B is 600 metres, then find the length of train A. (in metres)
A.
600
B.
480
C.
590
D.
900
😑 View Answer Rough Work
ANSWER :
B. 480
68.
An airplane goes 14 km due east and then 48 km due north. How far is it from its initial position?
A.
14 km
B.
48 km
C.
50 km
D.
28 km
😑 View Answer Rough Work
ANSWER :
C. 50 km
69.
If ∆ABC = ∆PQR and ∠ABC = (x + 60)°, ∠PQR = (85 - 4x)°, and ∠RPQ = (3x + 65)°, then the value of ∠ABC in degree is:
A.
15
B.
5
C.
45
D.
65
😑 View Answer Rough Work
ANSWER :
D. 65
70.
If the number 6788934a4 is divisible by 11, then find the smallest whole number in the place of a.
A.
3
B.
4
C.
5
D.
2
😑 View Answer Rough Work
ANSWER :
D. 2