If Mohit can complete \( \frac{2}{3} \) of a work in 24 days, then in how many days can \( \frac{1}{9} \) of the work be completed by him?
If \(
\left( x + \frac{1}{x} \right) = 2\sqrt{2}, \quad \text{and } x > 1,
\) what is the value of \( (x^6 - \frac{1}{x^6}) \)
140\(\sqrt{2}\)
116\(\sqrt{2}\)
144\(\sqrt{2}\)
128\(\sqrt{2}\)
If \(\frac{\sin x - \cos x}{\sin x + \cos x} = \frac{2}{5}\) then , what is the value of \(\frac{1 + \cot^2 x}{1 - \cot^2 x}\) is:
Study the given pie chart and answer the question that follows.
The pie chart displays the % of fruits sold(in kg) by fruit seller in one month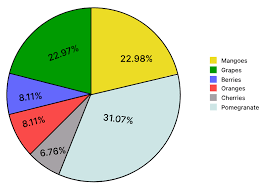
If the total fruits sold by a fruit seller in one month was 50,000 kg, find the approximate difference of the quantity (in kg) of pomegranates and that of berries.
Simplify the given expression
\(\frac{432 \times 432 + 247 \times 247 - 432 \times 247}{432 \times 432 \times 432 + 247 \times 247 \times 247}\)
\( \frac{1}{259} \)
\( \frac{1}{185} \)
\( \frac{1}{679} \)
\( \frac{1}{450} \)
Simplify the following.
\(\frac{3a + b}{2} - \frac{a - 3b}{3} + 2b\)
\(\dfrac{5(a + 3b)}{6}\)
\(\dfrac{7a + 3b}{6}\)
\(\dfrac{7(a + 3b)}{6}\)
\(\dfrac{a + 3b}{6}\)
On day one, with speed v, R covers a distance x, in t time. On the next day, he covers a distance 2.5x in 0.75t time. What is his speed the next day?