SSC CGL 2024-09.09.2024-3 SSC Question Paper

The mean proportional of 8a2 and 18/a4, where a is a positive number, is _______.

If then find the value of cosec α.

Ramesh has ₹18,000. He deposited ₹7,000 in a bank at the rate of 5% per annum and ₹6,000 in other bank at the rate of 6% per annum simple interest. If he received ₹1,160 as simple interest at the end of one year, then the rate of interest per annum on rest of the capital is equal to:

If the length, breadth, and height of a cuboid is 8 cm, 4 cm, and 6 cm, respectively, then the volume (in cm3) of the cuboid is:

The following table shows the sale (in thousands) of different types of helmets by a shop over the given years Type of Helmet / Year 1998 1999 2000 2001 2002 A 78 45 56 63 88 B 58 64 78 60 68 C 46 54 58 64 68 D 76 65 72 78 82 E 87 66 74 80 84 What was the percentage increase in the sale of Helmets C in 2002 as compared to that in 1999?

Study the given graph and answer the question that follows.
The graph shows the production of refrigerators by three companies in 2018. 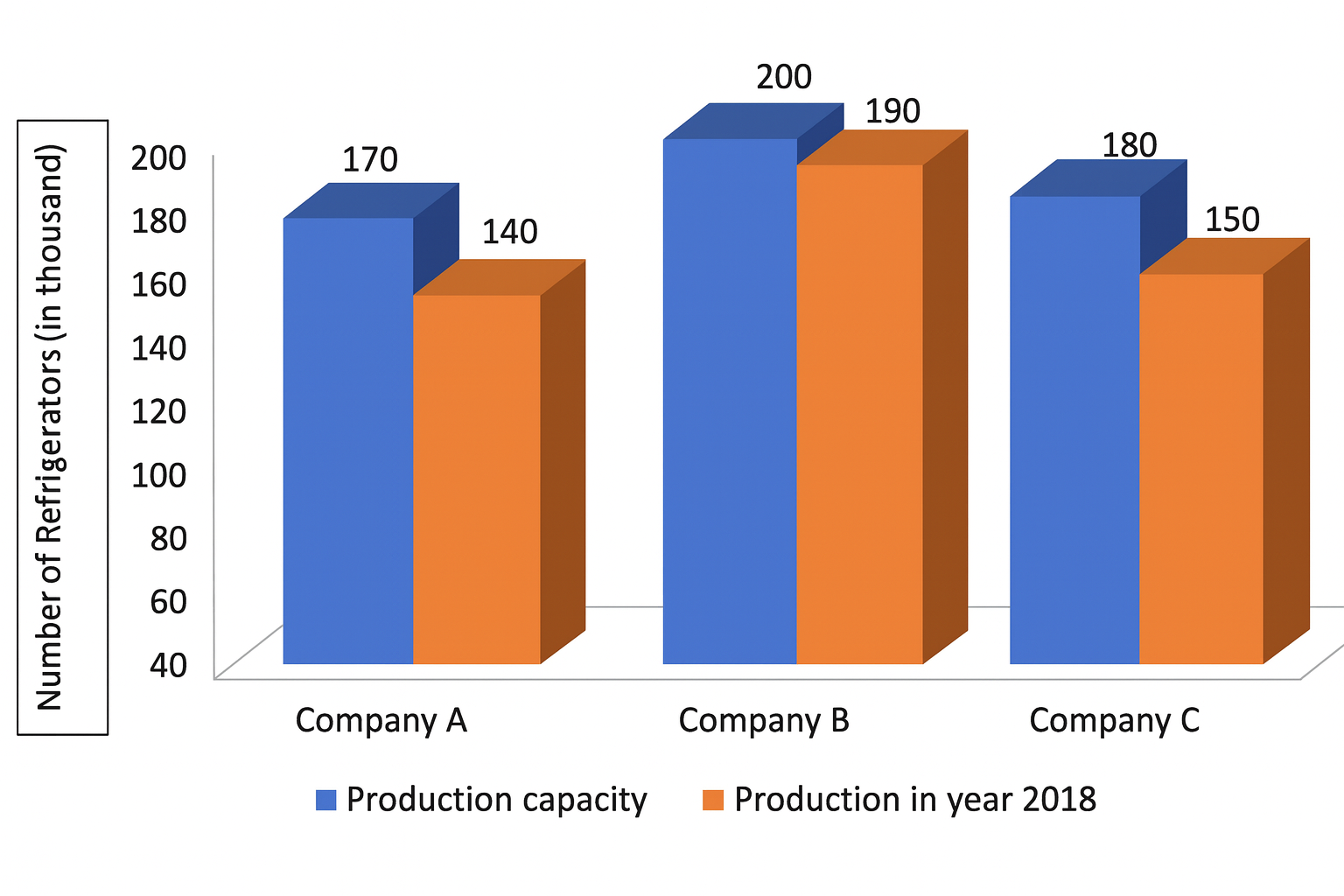The refrigerators produced by company C form what percentage of the total production?

What is the perimeter (in cm, rounded off to one decimal place) of the sector of a circle with a radius of 10 cm and of angle 30°?
(Use π = 3.14)

If 7845K854 is divisible by 11, then what is the value of K?

If A is an acute angle, which of the following is equal to

In a ΔPQR, the bisectors of∠Q and∠R meet at point O, inside the triangle. If∠QOR = 107°, then the measure of∠P is: