If \(\sqrt{x} + \frac{1}{\sqrt{x}} = 7\) then the value of \(x + \frac{1}{x}\) is equal to:
A merchant has 1000 kg of sugar, part of which he sells at a 10% profit and the rest at a 40% profit. He gains 20% on the whole. The quantity sold at 40% profit is:
\(543 \tfrac{1}{3} \text{ kg}\)
\(383 \tfrac{1}{3} \text{ kg}\)
\(333 \tfrac{1}{3} \text{ kg}\)
\(443 \tfrac{1}{3} \text{ kg}\)
Akshay purchased pens and notebooks from a shop for a total sum of ₹180. From the following data, what is the value of ‘X’?
| Items | Price per unit (in ₹) | Quantity |
| Pens | 10 | X |
| Notebooks | 20 | 6 |
Simplify \(\frac{0.58 \times 0.58 \times 0.58 - 0.001}{0.58 \times 0.58 + 0.058 + 0.01}\)
The given bar graph shows the production of bikes by a company (in thousands) over the years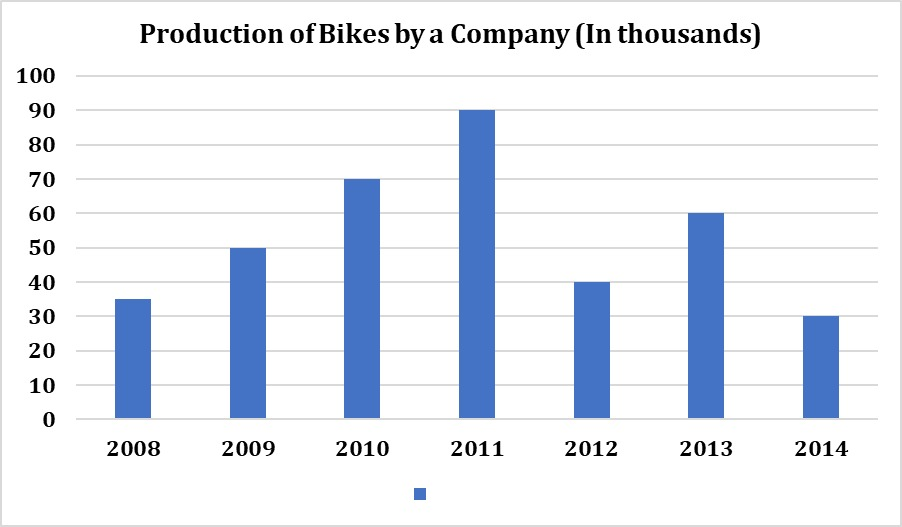
In how many of the given years was the production of bikes more than the average production of bikes over the years?.
If cotθ = \(\frac{4}{3}\) , then evaluate \(
\frac{\sec\theta \, (1 + \cot^2\theta) \, (\mathrm{cosec}^2\theta - \cot^2\theta)}{\mathrm{cosec}^3\theta}
\)
\(\frac{3}{4}\)
\(\frac{4}{5}\)
\(\frac{4}{3}\)
\(\frac{3}{5}\)