Quantitative Aptitude
The following table indicates the number of students studying in three subjects in four colleges.
What is the ratio of the total number of students studying in the Physics to that of studying in Mathematics in all four colleges taken together?
Colleges
Subjects W X Y Z
Physics 420 435 412 285
Chemistry 380 340 315 420
Maths 256 310 295 345
A chord of the larger among two concentric circles is of length 20cm and it is tangent to the smaller circle. What is the area (in cm2) of the annular portion between the two circles?
The given pie-chart shows the percentage distribution of runs scored by a batsman in a test innings. Study the chart and answer the question that follows.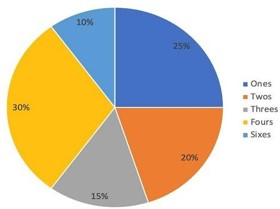
If the batsman has scored a total of 440 runs, how many runs did he score by hitting fours?
A trader owes a merchant ₹9,810 due in 1 year, but the trader wants to settle the account after 6 months. If the rate of simple interest is 9% per annum, how much cash (in ₹) should he pay?
The radius of the circle is 8 cm. The distance of a point lying outside the circle from the centre is 17 cm. The length of the tangent drawn from the outside point to the circle is:
