The given bar graph shows sugar imports of a country (in thousand tonnes) over the years. Study the graph and answer the question that follows.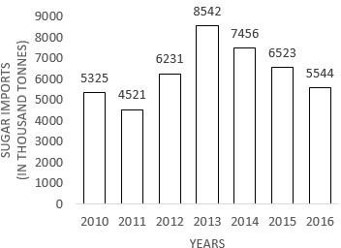
The average imports (in thousand tonnes) of all the years is:
The following table shows the number of pages printed by 3 printers (P, Q and R) for 3 days.
What is the ratio of the total number of pages printed by printer P over the course of three days to the total number of pages printed by printer Q during the same three days?
Day P Q R
Monday 100 130 200
Tuesday 120 145 160
Wednesday 180 85 120
The circumference of the base of the cylindrical vessel is 154 cm and its height is 49 mm. How many litres of water can it hold? (correct to three places of decimals, use π = (22/7)
The centres of two circles are 36 cm apart. If the radii of these two circles are 15 cm and 9 cm, respectively, then what is the sum of the lengths (in cm) of a direct common tangent and a transverse common tangent of these two circles?
Suppose P starts walking at a speed of 8 km/h. After 8 hours B started travelling on a bicycle at a speed of 24 km/h. The distance from the starting B can catch A is:
Ramesh purchased 130 books at the rate of ₹200 each and sold half of them at the rate of ₹300 each, one-fifth of them at the rate of ₹350 each and the rest at the cost price. Find his profit percentage.
